In many computer vision applications, it is important to extract special features from the image which are distinctive, unambiguously to locate and occur in different images showing the same scene. There is a complete subbranch in the computer vision field dedicated to this task: feature matching. Usually, this process consists of three tasks: detection, description and matching. I shortly want to summarize the steps but you can easily find further information on the web or in related books1.
- The first step is about the detection of distinctive points in an image. This could be a corner of an object, an intensity blob (e.g. the inner parts of the eyes) or any other special shape or structure you can imagine. Not good candidate points are e.g. straight lines. It is hard to detect a point on a line unambiguously in two images (which point on the line to choose?).
- The goal of the description step is to describe the area around a detected point. A lot of techniques can be used here and it is quite common to get a vector with some numbers which describe the area around the point as output. If two points have a similar surrounding, it would be good if the vectors would also have similar numbers.
- This is essential for the third and last step: matching. Imagine two images showing the same scene with a different viewpoint. In both images are distinctive points detected and the surrounding of each point described. Which points correspond, i.e. which points show the same part of the scene? This can e.g. be done by measuring the similarity between the description vectors.
For each of these steps, many different algorithms exist. As you may have guessed from the title of this article I want to focus here on the detection step. More precisely, I introduce the Hessian detector which is mathematically defined as:
An image is scaled to a size defined by the scale parameter \(\sigma\). Let \(H_{\sigma}\) denote the Hessian matrix at a specific image location in level \(\sigma\) and e.g. \(\partial_{xx} = \frac{\partial^2 I}{\partial^2 x^2}\) denoting the second order derivative of the image \(I\) along the \(x\)-axis. We can use the normalized determinant response of the Hessian
\begin{equation} \label{eq:HessianDetector_Definition} \sigma^4 \cdot \det(H_{\sigma}) = \sigma^4 \cdot \left( \partial_{xx} \cdot \partial_{yy} - \partial_{xy}^2 \right) \end{equation}to detect image features (blobs and notches) by searching for maxima in each image location across scale.
I just wanted to give the definition of the detector at the beginning; the intention of this article is to give some insights why this equation might indeed be useful. Also, note that the detector is designed to find blobs in an image (and not corners).
So, what exactly is a blob in an image? It is a homogeneous area with roughly equal intensity values compared to the surrounding. The ideal artificial example is a 2D Gaussian function where the intensity values equally decay in a circle way blending together with the surrounding – visible in the image as a smooth blob. A more realistic example would be the inner part of a sunflower which is usually dark compared to the bright leaves. The following figure shows examples for both. A blob is not necessarily related to a circle like structure though. Any kind of intensity notch may also be detected as a blob. And the idea is that these circles and notches are part of the object and therefore are also visible in other images showing the same object.


The rest of this article is structured as follows: I begin introducing the Hessian matrix, analyse the curvature information it contains and describes how this information is used in the Hessian detector. But I also want to talk a bit about how the detector incorporates in the scale space usually used in feature matching to achieve scale invariance.
The Hessian matrix
Let's start with the Hessian matrix \(H\) (scale index \(\sigma\) for simplicity omitted). Mathematically, this matrix is defined to hold the information about every possible second order derivative (here shown in the 2D case)3:
\begin{equation*} H = \begin{pmatrix} \frac{\partial^2 I}{\partial^2 x^2} & \frac{\partial^2 I}{\partial x \partial y} \\ \frac{\partial^2 I}{\partial y \partial x} & \frac{\partial^2 I}{\partial^2 y^2} \\ \end{pmatrix}. \end{equation*}Since \(\frac{\partial^2 I}{\partial x \partial y} = \frac{\partial^2 I}{\partial y \partial x}\) this matrix is symmetric4. Conceptually, \(H\) can be understood as the second order derivative of a higher dimensional function. As we know from the 1D case, the second order derivative tells us something about the curvature of a function: is it convex, concave or neither of those? The result here is a number where the signum function tells us which of the cases is true. But what is the curvature of a 2D function?
It turns out that things get more complicated when introducing another dimension (who on earth would have guessed that...). We can't express the curvature as a single number anymore since the question now is: how is the curvature in a certain direction? Imagine you are walking over an arête in the mountains where it goes down on the left and right side and straight on in front of you. What is the curvature when you keep moving ahead? Since there are not many changes in height probably (roughly) zero. And what if you move right directly downwards the precipice? Probably very high since there are a lot of changes in height. So, direction obviously matters.
To get the curvature of a 2D function we need to provide three parameters: the Hessian matrix \(H\), which acts as the curvature tensor containing the information about every direction, a specific direction \(\fvec{s}\) in which we are interested and the location \(\left( x_0, y_0 \right)^T\) where we want to know the curvature of. The direction is usually provided as uniform (i.e. \(\left\| \fvec{s} \right\|=1\)) column vector. We can then compute the so-called directional derivative
\begin{equation} \label{eq:HessianDetector_DirectionalDerivative} \frac{\partial^2 I}{\partial^2 \fvec{s}^2} = \fvec{s}^T H \fvec{s} \end{equation}which gives as the curvature (the second order derivative) in the direction \(\fvec{s}\). Before showing some visualization, I want to provide a numeric example. For this, consider the following 2D function and suppose you want to know the curvature in the \(45^{\circ}=\frac{\pi}{4}\) direction at the origin
\begin{equation*} f(x,y) = \cos(x), \quad \fvec{s} = \begin{pmatrix} \cos\left( \frac{\pi}{4} \right) \\ \sin\left( \frac{\pi}{4} \right) \end{pmatrix} \quad \text{and} \quad \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix}. \end{equation*}It is actually a bit stupid to call this a 2D function since it is just the standard cosine but the resulting graph fits nice to my arête analogy. The first thing to do is to calculate the derivatives of the Hessian matrix
\begin{align*} \frac{\partial^2 f(x, y)}{\partial^2 x^2} &= - \frac{\partial}{\partial x} \sin(x) = -\cos(x) \\ \frac{\partial^2 f(x, y)}{\partial x \partial y} &= 0 \\ \frac{\partial^2 f(x, y)}{\partial y \partial x} &= - \frac{\partial}{\partial y} \sin(x) = 0 \\ \frac{\partial^2 f(x, y)}{\partial x \partial y} &= 0 \end{align*}and summarize the results in the Hessian matrix
\begin{equation*} H = \begin{pmatrix} -\cos(x) & 0 \\ 0 & 0 \\ \end{pmatrix}. \end{equation*}Next, we apply \eqref{eq:HessianDetector_DirectionalDerivative} and get
\begin{align*} \frac{\partial^2 f}{\partial^2 \fvec{s}^2} = \fvec{s}^T H \fvec{s} &= \begin{pmatrix} \cos\left( \frac{\pi}{4} \right) & \sin\left( \frac{\pi}{4} \right) \end{pmatrix} \begin{pmatrix} -\cos(x) & 0 \\ 0 & 0 \\ \end{pmatrix} \begin{pmatrix} \cos\left( \frac{\pi}{4} \right) \\ \sin\left( \frac{\pi}{4} \right) \end{pmatrix} \\ &= \begin{pmatrix} \cos\left( \frac{\pi}{4} \right) & \sin\left( \frac{\pi}{4} \right) \end{pmatrix} \begin{pmatrix} -\cos(x) \cos\left( \frac{\pi}{4} \right) \\ 0 \end{pmatrix} \\ &= - \cos\left( \frac{\pi}{4} \right) \cos(x) \cos\left( \frac{\pi}{4} \right) \\ &= - \frac{1}{\sqrt{2}} \frac{1}{\sqrt{2}} \cos(x) \\ &= - \frac{\cos(x)}{2} \end{align*}i.e. a curvature of \(-\frac{1}{2}\) in the direction of \(\fvec{s}\) at our evaluation point \(x_0=0\) (origin).
You can imagine this as follows: at every point of our 2D function, we have a normal vector pointing orthogonal to the surface at that point. The normal vector forms together with the direction \(\fvec{s}\) a plane in the 3D space. This plane intersects with our function resulting in a projection which is a 1D function and \eqref{eq:HessianDetector_DirectionalDerivative} is then just the curvature of this function (like from every other 1D function). The following animation shows the discussed points and lets you choose an arbitrary direction.
Even though this is very exciting, one is often not interested in the curvature of an arbitrary direction. What is more of interest is the direction of highest and lowest curvature. The good news is that it is also possible to retrieve this information from \(H\). The information lies in the eigenvectors and eigenvalues: the eigenvector \(\fvec{e}_1\) points in the direction of the highest curvature with the magnitude \(\lambda_1\). Similarly, \(\fvec{e}_2\) corresponds to the direction of lowest curvature with the strength of \(\lambda_2\)5. As you may have noticed, I already included \(\fvec{e}_1\) in the previous animation. Can you guess in which direction \(\fvec{e}_2\) points and what the value of \(\lambda_2\) is?6
For a 2D function, this means that we can obtain two orthogonal vectors pointing in the highest and lowest direction. The following animation has the aim to visualize this. In order to make things a little bit more interesting, I also used a different function: \(L(x,y)\). This is now a “proper” 2D function, meaning that both variables are actually used. It is essentially a linear combination of Gaussian functions building a landscape; therefore, I called it Gaussian landscape7.
Take your time and explore the landscape a bit. A few cases I want point to:
- If you are at the centre of the Gaussian blob (bottom left corner, \(\left( -10, -10 \right)^T\), did you notice that both eigenvalues are equal (\( \left| \lambda_1 \right| = \left| \lambda_2 \right| \))? This is because the curvature is the same in every direction so there is no unique minimal or maximal direction. This is for example also true for every point on a sphere.
- When you are on the ground, e.g. at position \(\left( -6, -6\right)^T\), there is no curvature at all (\( \left| \lambda_1 \right|, \left| \lambda_2 \right| \approx 0\)). This is true for every point on a planar surface.
- Another fact is already known from the previous animation: when you walk alongside the arête (e.g. at position \(\left( 0, -5\right)^T\)), the magnitude of the first eigenvalue is high whereas the second is roughly zero (\( \left| \lambda_1 \right| > 0, \left| \lambda_2 \right| \approx 0\)). This is for example also true for tube-like objects (e.g. a cylinder).
- Last but not least, when you descent from the hill (e.g. at position \(\left( 0, -9\right)^T\)) there is curvature present in both directions but the first direction is still stronger (\( \left| \lambda_1 \right| > \left| \lambda_2 \right| > 0\)). This is a very interesting point, as we will see later.
What has this to do with blobs in an image? Well, the first and last case I have just pointed out fall directly into the definition of a blob whereas the first one is more circle-like and the last one is more notch-like. Since we want to detect both cases, it does not really matter which one we have. One way to detect these cases based on the eigenvalues is by using the Gaussian curvature
\begin{equation} \label{eq:HessianDetector_GaussianCurvature} K = \lambda_1 \cdot \lambda_2. \end{equation}The main observation is that this product is only large when both eigenvalues are large. This is true for the first and fourth case and false for the other two since the product is already low when \( \left| \lambda_2 \right| \approx 0\) (note that it is assumed that the eigenvalues are descendingly sorted, i.e. \( \left| \lambda_1 \right| \geq \left| \lambda_2 \right| \)).
We can now detect blobs at each image position by calculating the Hessian matrix via image derivatives, their eigenvalues and then the Gaussian curvature \(K\). Wherever \(K\) is high we can label the corresponding pixel position as a blob. However, “wherever something is high” is not a very precise formulation, and, usually, comes with the cost of a threshold in practice. Since we have also a strength of the blob (the determinant response) we can easily overcome this by using only the largest blobs in an image and these are the local maxima of \(K\). It is e.g. possible to sort the local maxima descendingly and use the \(n\) best (or define a threshold, or use just every maximum, or do something clever).
But wait a moment, when \eqref{eq:HessianDetector_GaussianCurvature} is already the answer to our initial problem (finding blobs) why does \eqref{eq:HessianDetector_Definition} use the determinant of \(H\) and this strange \(\sigma^4\) prefactor? The second part of this question is a bit more complicated and postponed to the next section. But the first part of this question is easily answered: there is no difference, since the equation
\begin{equation*} \det(H) = \lambda_1 \cdot \lambda_2 \end{equation*}holds. This means that \eqref{eq:HessianDetector_Definition} already calculates the Gaussian curvature. Before moving to the discussion of the scale parameter though, I want to show the result when the determinant of the Hessian is applied to the Gaussian landscape.
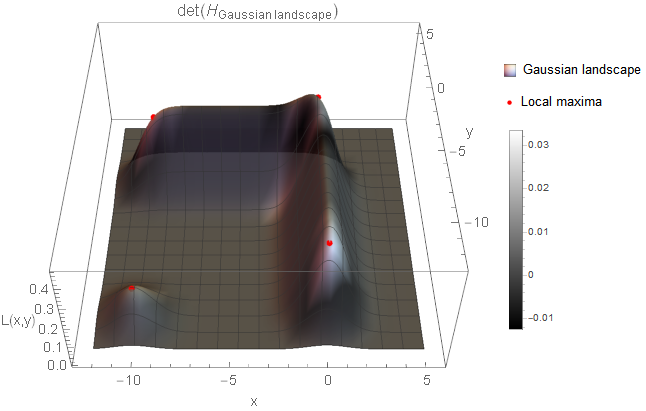
As you can see, the determinant response clearly separates our landscape with the maxima identifying locations which are either circle-like (bottom left) or notch-like (rest) blobs. Next, I want to apply this technique to a real image.

Notice the small intensity blobs present in the original image which are very well captured by the determinant response (e.g. the small white dots in the bottom of the image). Even though we can now detect some relevant parts of the image, did you notice that other parts are not detected? Especially the larger blobs like the round structure in the top right corner of the image. This is where the scale normalization parameter \(\sigma\) gets important. But before dealing with it, I want to analyse one aspect of the curvature a bit further.
What about the sign of the eigenvalues?
There is one detail which I have left out so far: the eigenvalues obtained from the Hessian matrix \(H\) do have a sign and you may notice that I used the absolute values \( \left| \lambda_i \right|\) when comparing the eigenvalues of the Gaussian landscape. Further, we only searched for maxima and not minima in the determinant response. Before deciding whether the sign is important or not, let's analyse the curvature of a one-dimensional Gaussian in order to understand what the sign actually means.
The following figure shows a Gaussian function \(g(x)\) together with its second order derivative, i.e. the curvature. Besides the normal Gaussian (which is called positive) also a negative Gaussian is shown. The later is just an inverted version which has a hole in the middle instead of a peak. In an image, the positive Gaussian corresponds to a white blob on a dark background and the negative Gaussian to a black blob on a white background (both is possible and we want to detect both).
The interesting part is the second order derivative. For the positive Gaussian, it starts with a low left curvature, changes to a strong right curvature in the middle and reverts back to a low left curvature. You can observe three extrema but only one of them is high and corresponds to the blob we want to detect. In case of the negative Gaussian, the strong peak corresponds to a maximum instead of a minimum. So, you may wonder why we search for a maximum then if both are possible. Remember that this is only a one-dimensional view and for images, we have a second dimension and deal with the curvature of the two main directions. Since we are only interested in detecting occurrences of the high extrema, there are three cases to consider for the second order derivative:
- We have a maximum in both directions, i.e. \(\lambda_1 > 0\) and \(\lambda_2 > 0\).
- We have a minimum in both directions, i.e. \(\lambda_1 < 0\) and \(\lambda_2 < 0\).
- We have a minimum in one and a maximum in the other direction, e.g. \(\lambda_1 < 0\) and \(\lambda_2 > 0\).
I created an example for each of the cases based on Gaussian functions \(g\). All two-dimensional plots are coloured based on the determinant response.
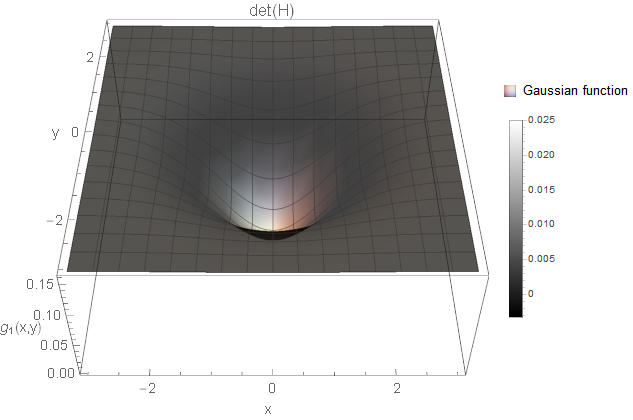
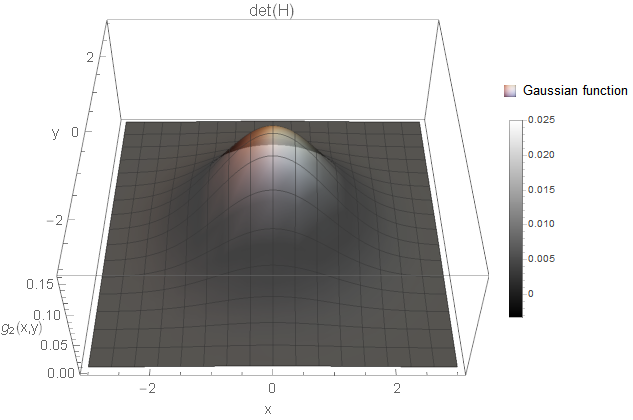
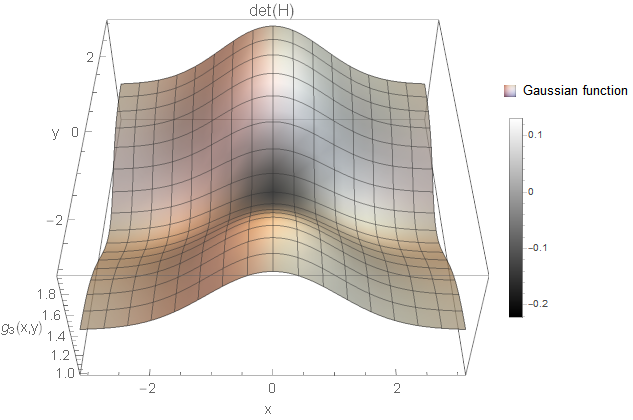
We certainly want to detect holes and blobs in the image (and corresponding notches). So, the first two cases are something we want to consider. But what about the third case? Is this a structure of interest? It is a white and a black line crossing smoothly with each other. Not sure what kind of image structure we can imagine for this but from the implementations I know, these curvature points are simply ignored. You could also argue that you detect rather the four white blobs surrounding the black blob instead (not as strong as the black blob, but still). Hence, it might not be necessary to search for this case after all (however, there might be applications where this case is of interest).
Ok, let's agree on detecting only the first two cases. We still have a maximum in one and a minimum in the other case. Is this a problem? Well, remember that the definition of the Gaussian curvature (\eqref{eq:HessianDetector_GaussianCurvature}) multiplies the two eigenvalues. For our two cases this means we either multiply two negative or two positive values with each other, i.e. we definitively end up with a positive value. This mystery solved, we can now move on to the discussion of the scale parameter \(\sigma\).
Scale normalization
So, the first important observation is that blobs may occur in different sizes. This was already the case for the sunflower image at the beginning. Not all sunflowers have the same size, and, additionally, they project to different sizes on the camera depending on the distance to the camera. What we want to achieve is a so-called scale invariance: blobs should be detected regardless of the size they occupy in the image.
But how can we achieve scale invariance? The answer is to build a scale space, e.g. by blurring the image repeatedly with a Gaussian function. The result is a scale pyramid with a different intrinsic image resolution on each level. This resolution is denoted by a \(\sigma_i\) parameter per level \(i\) which corresponds to a Gaussian function \(G_{\sigma_i}\) used to create the level (via convolution, i.e. \(I*G_{\sigma_i}\)). With increasing scale level the \(\sigma_i\) value also increases and the image is blurred more intense.
Our extrema search is therefore extended by an additional dimension: we can now search for maxima in the determinant response not only spatially in the image but also across scale in different resolutions of the same image. At each position, we can consider our determinant response also as a function of scale and pick the scale level with the highest response. But before we can do that we first need to solve a problem.
The thing is that the Gaussian blurring flattens the intensities in the image out since in each blurring step the intensity values come closer together due to the weighting process. Per se this is not a problem and is precisely the job of Gaussian blurring: flatten out outliers to create a smooth transition between the values. But the weighting process also decreases the possible range of values. If we, for example, start with an image where the range of intensity values lies in \([10;20]\) then after the blurring this range must be smaller, e.g. \([12;17]\) (depending on the distribution of the values and the precise \(\sigma_i\) value). At the end when we use a really high \(\sigma_i\) value, we have only one flat surface left with exactly one intensity value remaining and this is the average intensity of the first image (this is because the convolution with a Gaussian converges to the average image value).
Ok, but why is this now a problem? The fact is that when the intensity range decreases over scale it is also very likely that the derivative values will decrease (fewer changes) and hence the determinant response decreases. But when the determinant responses tend to get lower in higher scale levels we introduce a systematic error while searching for extrema across scale. Responses from higher levels will always have the burden of being computed based on a smaller intensity range compared to the first scale levels of the pyramid. Note that this does not mean that a response value for a specific location strictly decreases over scale. It is still possible that locally a new blob structure is detected which produces (slightly) higher response values than the previous level. But is it correct and significant? To find out, we must find a compensation for the decreased intensity range and we need to compensate more as higher we climb in our scale pyramid.
The idea is to use the \(\sigma_i\) values for compensation. Since they increase with higher scales, they fit our requirements. And this is exactly the reason why \eqref{eq:HessianDetector_Definition} contains \(\sigma^4\) as prefactor9 which stretches our intensity range again to be (roughly) equal as before the blurring process (e.g. \([10.4;19.7]\) instead of \([12;17]\); don't expect exact results in a noisy and discrete world). This makes the determinant response \(\det(H_{\sigma})\) comparable across scale. With this problem now solved we can move on and detect extrema over scale. For this, consider the following figure which shows the determinant response for the position in the blob of the top right corner of the airport image (also labelled in the image below).
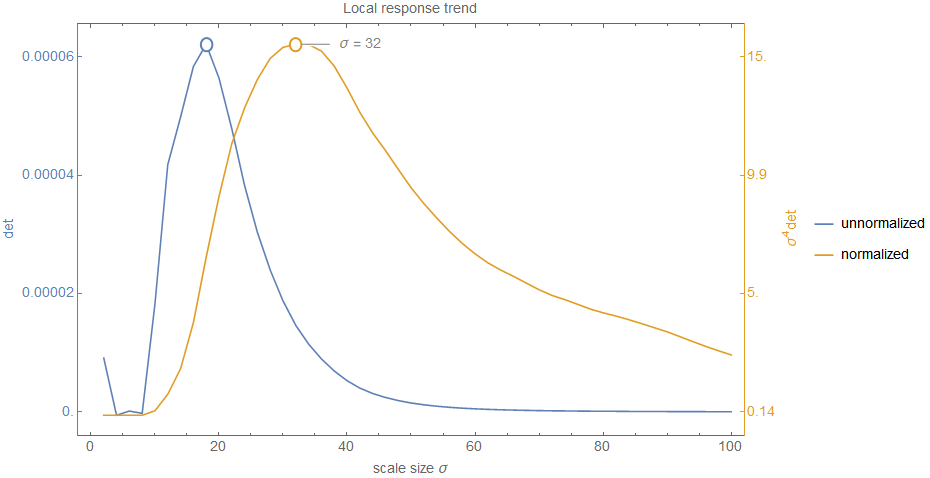
Technically, we have a unique maximum in both cases. Even when we do not normalize we get a peak. However, it is not as wide as in the normalized case. But back to the question: is this peak correct and significant? To answer the question let me emphasize that this is only the trend for a specific location and when you look at the original image you see that in a very fine scale space there is just a white area (i.e. roughly zero determinant response). But when increasing scale the borders of the circle-like blob get visible and we have therefore an increase in response. This doesn't answer the question about correctness and significance, though. For this, let's consider the following figure which shows the global response range for all response values in all locations over scale for both cases.
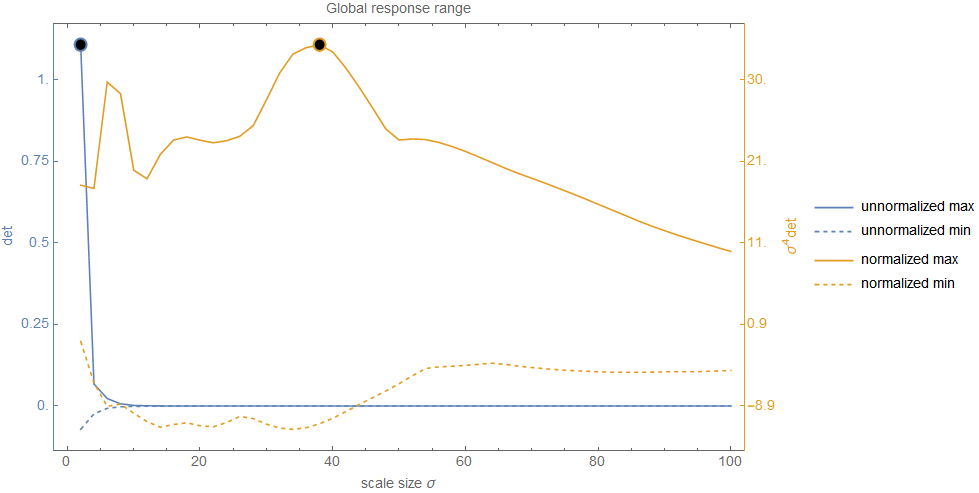
This graph shows very clearly what I meant with the decrease of response over scale when no normalization is used. In this case, we start with a large range in the first levels but the range narrows very fast to a nearly zero wide range. This explains why the magnitude of the response values was so low in the previous figure (e.g. only about 0.00006 at the peak) and really reinforces doubts about the correctness and significance of the peak. However, the range of the normalized response gives a different picture. Even though the range does not stay fixed (but this wasn't expected and highly depends on the example image), it's width remains rather solid. No strict decay and the values do not get ridiculously small. This shows very clearly that scale normalization is indeed important. To come back to the question about significance: it is obvious that any comparison between the unnormalized values can't lead to correct results and hence any extrema detected in this range is certainly not significant.
To answer the question about correctness and significance also numerically for a specific example, let's compare the maximum response from our specific location \((x_0,y_0)=(532, 98)^T\) with the global maximum response of all locations in all scale levels10
\begin{align*} \frac{ \max_{i=1,\ldots,50}(\det(H_{\sigma_i}(532, 98))) }{ \max_{i=1,\ldots,50}(\det(H_{\sigma_i})) } &= % MathJax offers a way to apply css to math elements: http://docs.mathjax.org/en/latest/tex.html#html % The math must contain a symbol, i.e. it should not be empty. Therefore, an arbitrary symbol is printed with the same colour as the face of the circle \frac{ \style{border: 2.2px solid #5e81b5; border-radius: 50%; background: white; width: 0.6em; height: 0.6em;}{\color{white}{o}} } { \style{border: 2.2px solid #5e81b5; border-radius: 50%; background: black; width: 0.6em; height: 0.6em;}{\color{black}{o}} } = \frac{0.0000621447}{1.10636} = 0.0000561703 \\ \frac{ \max_{i=1,\ldots,50}(\sigma_i^4 \cdot \det(H_{\sigma_i}(532, 98))) }{ \max_{i=1,\ldots,50}(\sigma_i^4 \cdot \det(H_{\sigma_i})) } &= \frac{ \style{border: 2.2px solid #e19c24; border-radius: 50%; background: white; width: 0.6em; height: 0.6em;}{\color{white}{o}} } { \style{border: 2.2px solid #e19c24; border-radius: 50%; background: black; width: 0.6em; height: 0.6em;}{\color{black}{o}} } = \frac{15.3165}{34.6083} = 0.442567. \end{align*}The idea behind this is that we need to compare different response values over scale for extrema detection and this relation measures how near the values are to each other. If values across scale do not operate in the same domain, a comparison is not really useful. This is like comparing distance values but one is measured in metres and the other kilometre. Since the value denoted in metre is naturally higher than the value denoted in kilometre, any comparison operation we perform on these values is prone to errors. As you can see from the calculated values, this is true for the maximum response without normalization as it is absolutely not significant and hence does not represent a correct extremum. On the other hand, the normalized response does not suffer from a huge difference between the values and therefore I would conclude this to be a very significant and correct extremum.
To finish up, let's take a look at the response image for the different scale levels. In order to make responses across scale visually comparable and to achieve a better image contrast, I scaled each response with the minimum and maximum value over all scale levels and all pixel locations, i.e. the response image \(R_{\sigma_i}\) for the scale size \(\sigma_i\) is calculated as
\begin{equation} \label{eq:HessianDetector_ResponseImageScale} R_{\sigma_i} = \frac{ \sigma_i^4 \cdot \det(H_{\sigma_i}) - \min_{i=1,\ldots,50}(\sigma_i^4 \cdot \det(H_{\sigma_i})) } { \max_{i=1,\ldots,50}(\sigma_i^4 \cdot \det(H_{\sigma_i})) - \min_{i=1,\ldots,50}(\sigma_i^4 \cdot \det(H_{\sigma_i})) }. \end{equation}This way all response values stay in \([0;1]\) and a response value of e.g. 0.4 means the same in all images, i.e. does not depend on the current scale level. But this formula is only used to achieve a better visualization; feel free to ignore it.
As you can see, the blob at our location of interest \((x_0,y_0)=(532, 98)^T\) is now detected and \(\sigma_{16}=32\) gives indeed a fairly strong response. With the same technique we can also detect other blobs: find the maximum determinant response across scale for each image position.
This was also the last part of our journey which started with \eqref{eq:HessianDetector_Definition} were we took a deep breath at the Hessian matrix and analysed the curvature information it contains. We moved forward while keeping the Gaussian curvature \(K\) in our bag, making sure signs don't cross our way and used \(K\) to find extrema responses in the image. We needed to take a break and first got around about correct scale normalization. This problem solved via the \(\sigma_i^4\) prefactor, we could search for extrema over the complete scale pyramid and so the circle completed again with \eqref{eq:HessianDetector_Definition}.
List of attached files:
- HessianDetector_ExampleGaussianBlob.nb [PDF] (Mathematica notebook which I used to create the Gaussian blob image)
- HessianDetector_HessianCurvature.nb [PDF] (Mathematica notebook which contains the analysis of the curvature information embedded in the Hessian matrix, e.g. it contains the first two animations I used here)
- HessianDetector_DeterminantResponse.nb [PDF] (Mathematica notebook for the calculation of the determinant response; both on the Gaussian landscape and on the airport image. Contains also the figures for the local response trend and global response range)
- HessianDetector_CurvatureSign.nb [PDF] (Mathematica notebook analysing the sign of the eigenvalues)

