When you have worked with images in OpenCL before, you may have wondered how to store them. Basically, we have the choice between using buffers or image objects. The later seems to be designed for that task, but what are the differences and how do they perform differently when applying a certain task? For a recent project, I needed to decide which storage type to use and I want to share the insights here. This is a follow-up article to my previous post where I already evaluated filter operations in OpenCL.
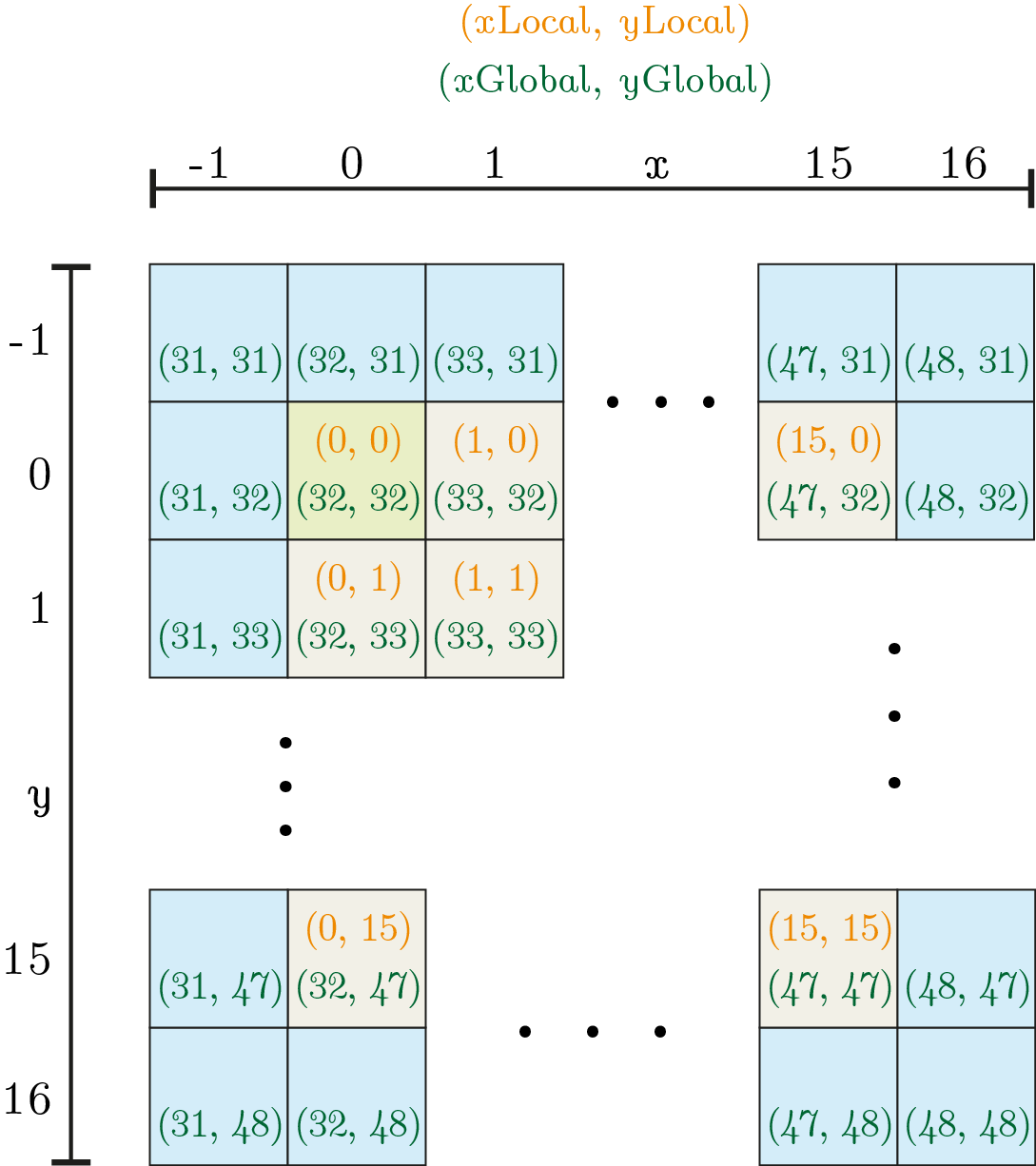
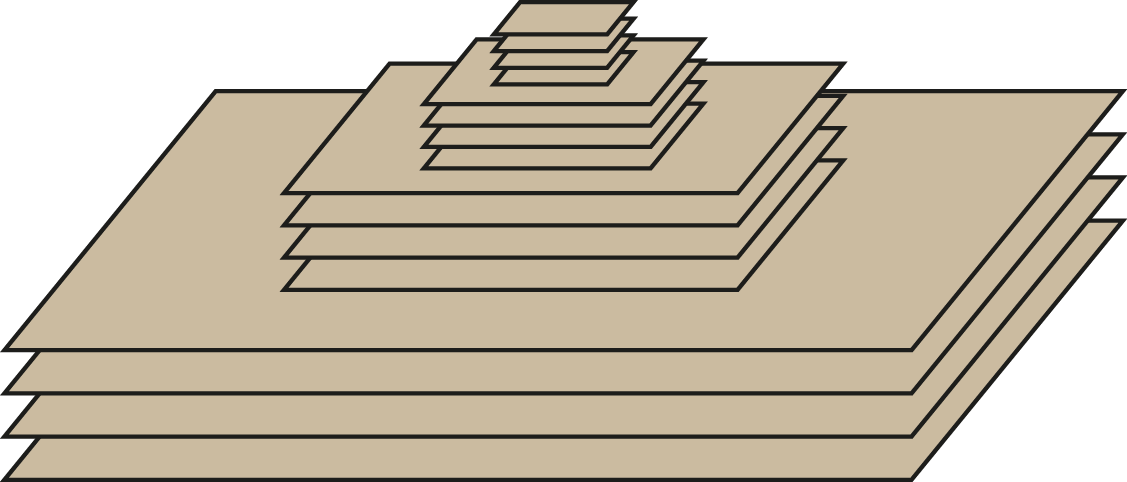
I did not only need to store plain images but rather a complete image pyramid, like visualized in the following figure, originating from a scale space. The pyramid consists of four octaves with four images each making up 16 levels in total. In each octave, the size of the images is always the same. With my used example image, the four images in the first octave have the size of the base image which is \(3866 \times 4320\) pixels. \(1933 \times 2160\) pixels are used in the second, \(966 \times 1080\) in the third and \(483 \times 540\) in the fourth octave making up a total of 88722000 pixels.
In order to measure the performance for the best storage types to use for the image pyramid, I applied image convolution with two derivative filters (Scharr filters) to the complete pyramid testing with the filter sizes of \(3 \times 3\), \(5 \times 5\), \(7 \times 7\) and \(9 \times 9\). I decided to assess four storage types for this task:
- Buffer objects are basically one-dimensional arrays which can store any data you want. All pixel values of the image pyramid are stored as a one-dimensional array with a length of 88722000 in this case. This introduces overhead in the access logic, though, since the pyramid is by its nature not one-dimensional but rather three-dimensional with a non-uniform structure, i.e. not all images in the pyramid have the same size. I use a lookup table to minimize the overhead during computation. However, there is still the overhead for the programmer which needs to implement the logic.
- Image buffer objects are created from buffers (so a
cl::Bufferobject is additionally necessary on the host side) and are offered by convenience to use a buffer which behaves like an image. However, it is very limited and can e.g. not be controlled by a sampler object. But it turns out that it is sometimes faster than buffers on my machine as we will see later. In theory, it would also be possible to use one-dimensional images (e.g.image1d_tin the kernel code) but this type of object is limited to the maximum possible width of a 2D image object (16384 on my machine) and hence not suitable to store an image pyramid with 88722000 pixels. Image buffers are not under this constraint but rather restricted by theCL_DEVICE_IMAGE_MAX_BUFFER_SIZEvalue (134217728 on my machine). - Images are a special data type in OpenCL which can be one-, two- and three-dimensional. The 16 levels of the image pyramid are stored as 16 image objects, e.g. as
std::vector<cl::Image2D>. Handling of this object type is easiest for the programmer and as it will turn out is also very fast and I ended up using this storage type for my project. - Cubes are very similar to image types. They basically add a third dimension to the image objects. The idea here is that each octave, where all images have the same size, is stored in one cube resulting in four cubes in total. The overhead should be less for cubes than for images but I could not confirm this definitively in the benchmarks below hence I did not use this type.
The idea behind the four storage types is also visualized in the following figure.
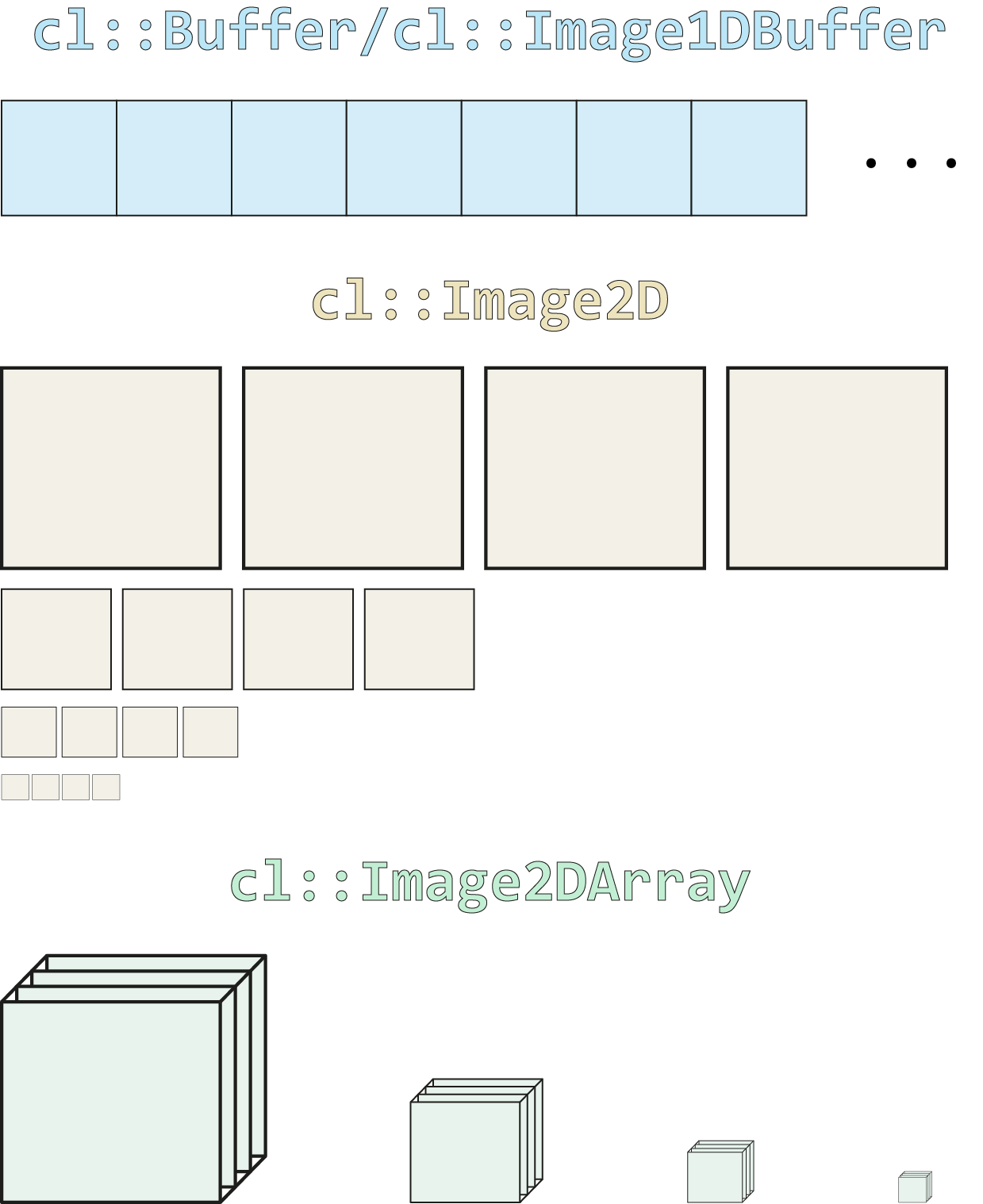
The four types and their properties are also summarized in the table below.
| Storage type | Host side type | Kernel side type | Kernel calls |
|---|---|---|---|
| Buffer | cl::Buffer |
global float* |
4 |
| Image buffer | cl::Image1DBuffer |
image1d_buffer_t |
4 |
| Images | cl::Image2D |
image2d_t img |
16 |
| Cubes | cl::Image2DArray |
image2d_array_t img |
4 |
The column with the kernel calls denotes how often the OpenCL kernel must be executed in order to apply one filter to the complete image pyramid. Images need the most since the filter kernel must be applied to each image layer in the pyramid individually. The other types contain the notion of an octave in the pyramid and hence know that four images have the same size. It is, therefore, possible to apply the filter function to the complete octave at once.
Before diving into the benchmark though, I want to describe a bit the hardware details about the differences between buffers and images. Note that I use an AMD R9 290 @ 1.1 GHz GPU in the benchmark and hence concentrate only on the GCN architecture.
Buffer vs. images in the hardware context
It is not very easy to find detailed information about how the different storage types are handled by the hardware (or I am too stupid to search). But I will present my findings anyway.
The most important note is that image objects are treated as textures in the graphics pipeline. Remember that GPUs are designed for graphics tasks and the thing we do here in GPGPU with OpenCL is more the exception than the rule (even though it is an important field). Textures are a very important part of computer graphics and when you have ever developed your own (min)-game you know how fruitful this step is. As soon as textures are involved the whole scene does look suddenly much better than before. It is therefore only natural that the hardware has native support for it.
In computer graphics, a lot of tasks need to be done related to textures, e.g. texture mapping. This is the process where your images are mapped to the triangles in the scene. Hence, the hardware needs to load the necessary image pixels, maybe do some type conversion (e.g. float to int) or even compression (a lot of textures need a lot of space) and don't forget address calculations, interpolating as well as out-of border handling. To help with these tasks, the vendors add extra texture units which implement some of the logic in hardware. This is also visible in the block diagram of a compute unit of the AMD R9 290
As you can see, the transistors responsible for textures are located on the right side. There are four texture units (green horizontal bars) where each unit is made up of one filter unit and four address units. Why four times more address units than filter units? I don't know if this was the design choice but I would guess that this has something to do with bilinear interpolation where four pixels are needed to calculate one texel. It is also possible that this has something to do with latency hiding and hardware parallelism. Memory fetches may need a lot of time compared to the execution of ALU instructions in the SIMD units. In order to stay busy, the hardware executes multiple threads at once so that while one thread still waits for the data the others can already start with execution. But each thread needs data and must issue memory requests hence multiple store and load units are necessary. Note that these texture units are located on each compute unit and are not shared on a per-device basis. My device has 40 compute units so there are 160 texture units in total.
The address units take the requested pixel location, e.g. an \(x\) and \(y\) coordinate, and calculate the corresponding memory address. It could be possible that they do something like \(cols*y + x\) to calculate the address. When interpolation is used, the memory addresses for the surrounding pixels must be calculated as well. Anyway, requests to the memory system are issued and this involves the L1 cache (16 KB) next to the address units. This cache is sometimes also called the texture cache (since it holds texels).
Since the cache is shared between all wavefronts on the compute unit, it offers an automated performance gain when the wavefronts work on overlapping regions of the same data. E.g. in image convolution the pixels need to be accessed multiple times due to the incorporation of the neighbourhood. When the wavefronts on the compute unit process neighbouring image areas, this can speed up the execution since less data needs to be transferred from global to private memory. It is loaded directly from the cache instead.
There is also a global L2 texture cache with a size of 1 MB which is shared by all compute units on the device. Usually, the data is first loaded in the L2 cache before it is passed to the L1 caches of the compute units. In case of image convolution, the L2 cache may hold a larger portion of the image and each compute unit uses one part of this portion. But there is an overlap between the portions since pixels from the neighbourhood are fetched in the image convolution operation as well.
Buffers and image objects are also accessed differently from within OpenCL kernel code. Whereas a buffer is only a simple pointer and can be accessed as (note also how the address calculation is done in the kernel code and hence executed by the SIMD units)
kernel void buffer(global float* imgIn, global float* imgOut, const int imgWidth)
{
const int x = get_global_id(0);
const int y = get_global_id(1);
float value = imgIn[imgWidth * y + x];
//...
imgOut[imgWidth * y + x] = value;
}
i.e. directly without limitations (it is just a one-dimensional array), image objects need special built-in functions to read and write values:
// CLK_ADDRESS_CLAMP_TO_EDGE = aaa|abcd|ddd
constant sampler_t sampler = CLK_NORMALIZED_COORDS_FALSE | CLK_ADDRESS_CLAMP_TO_EDGE | CLK_FILTER_NEAREST;
kernel void images(read_only image2d_t imgIn, write_only image2d_t imgOut)
{
const int x = get_global_id(0);
const int y = get_global_id(1);
float value = read_imagef(imgIn, sampler, (int2)(x, y)).x;
//...
write_imagef(imgOut, (int2)(x, y), value);
}
So, the function read_imagef(image2d_t image, sampler_t sampler, int2 coordinates) is needed to access the pixels. This is necessary so that the hardware can optimize the code and make use of the texture units where the sampler is used to configure it. But how can the cool functions I promised before now be used in OpenCL or equivalently: how to set up the texture filter units to do what we want?
- Interpolating: set the sampler to
CLK_FILTER_LINEARfor bilinear andCLK_FILTER_NEARESTfor nearest neighbour filtering. The additional texels are loaded automatically and the interpolated value is returned. If you need this interpolating functionality, you can also store other data than pixels in the image objects and get automatic interpolation. - Out-of-border handling: set the sampler e.g. to
CLK_ADDRESS_CLAMP_TO_EDGEto repeat the last values or use one of the other constants. The modes are a bit limited when not using normalized coordinates, though; but still, better than nothing. - Type conversion: this is controlled by the used function in the kernel. Above
read_imagefwas used which returns a float value. Use e.g.read_imageito return an int. Note that the functions in the kernel are independent of the real format set up on the host side.
How do buffer objects now differ? They don't use the texture units for a start since we do not provide a sampler object and do not use the built-in access functions. But they also use the cache hierarchy (bot L1 and L2) according to the docs. The programming guide by AMD states on page 9 “Actually, buffer reads may use L1 and L2. [...] In GCN devices, both reads and writes happen through L1 and L2.” and in the optimization guide on page 14 they claim further “The L1 and L2 read/write caches are constantly enabled. Read-only buffers can be cached in L1 and L2.”. This sounds for me that both caches are used for buffers as well but the benchmark results below suggest that a cache-friendly local work-group size seems to be important.
Regarding performance of the different memory locations, the general relationship is global > texture cache > local > private (cf. page 13ff of the optimization guide for some numbers). So even when image objects and hence texture cache is used, it may still be beneficial to explicitly cache data which is needed more than once by using the local data share (located in the centre in the block diagram). It is not surprising that global memory is the slowest and private memory the fastest. The trick is to reduce the time needed to transfer the data in the private registers of the SIMD units.
Implementation details
The buffer object is stored as a very long array in memory, but we still need to access locations in one of the images of the pyramid. But when we have only access to the 1D array from within the kernel, how do we write to a certain pixel location, let's say point \(p_1 = (10, 2)\) in level 9 of the pyramid? I decided to use a lookup table which is implemented as an array of structs defined as
struct Lookup
{
int previousPixels;
int imgWidth;
int imgHeight;
};
The most important information is previousPixels which gives the number of pixels from all previous images and hence is the start offset for the buffer to find the pixel in the considered image. Helper functions to read and write to a certain pixel location can now be defined as
float readValue(float* img, constant struct Lookup* lookup, int level, int x, int y)
{
return img[lookup[level].previousPixels + lookup[level].imgWidth * y + x];
}
void writeValue(float* img, constant struct Lookup* lookup, int level, int x, int y, float value)
{
img[lookup[level].previousPixels + lookup[level].imgWidth * y + x] = value;
}
E.g. for \(p_1\) the memory address is calculated as lookup[8].previousPixels + lookup[8].966 /* = 3866 / 4 */ * 2 + 10. The lookup array is filled on the host side and transferred to the GPU as an argument to the filter kernel. The following snippet does the computation on the host side and includes an example.
/*
* The following code generates a lookup table for images in a pyramid which are located as one long
* buffer in memory (e.g. 400 MB data in memory). The goal is to provide an abstraction so that it is
* possible to provide the level and the pixel location and retrieve the image value in return.
*
* Example:
* - original image width = 3866
* - original image height = 4320
* - image size in octave 0 = 3866 * 4320 = 16701120
* - image size in octave 1 = (3866 / 2) * (4320 / 2) = 4175280
* - image size in octave 2 = (3866 / 4) * (4320 / 4) = 1043820
* - number of octaves = 4
* - number of images per octave = 4
*
* Number of pixels for image[8] (first image of octave 2):
* - pixels in previous octaves = 4 * 16701120 + 4 * 4175280 = 83505600
* - previous pixels for image[8] = 83505600
*
* Number of pixels for image[9] (second image of octave 2):
* - pixels in previous octaves = 4 * 16701120 + 4 * 4175280 = 83505600
* - previous pixels for image[9] = 83505600 + 1043820 = 84549420
*/
locationLoopup.resize(pyramidSize);
int previousPixels = 0;
int octave = 0;
for (size_t i = 0; i < pyramidSize; ++i)
{
locationLoopup[i].previousPixels = previousPixels;
// Store size of current image
locationLoopup[i].imgWidth = static_cast<int>(img.cols / pow(2.0, octave));
locationLoopup[i].imgHeight = static_cast<int>(img.rows / pow(2.0, octave));
// The previous pixels for the next iteration include the size of the current image
previousPixels += locationLoopup[i].imgWidth * locationLoopup[i].imgHeight;
if (i % 4 == 3)
{
++octave;
}
}
The same technique is used for the image buffers as well. When it comes to enqueue the kernel at the host side, the following code is executed for each octave.
//...
const size_t depth = 4;
const int base = octave * depth; // octave is given as function argument
const size_t rows = lookup[base].imgHeight;
const size_t cols = lookup[base].imgWidth;
//...
const cl::NDRange offset(0, 0, base);
const cl::NDRange global(cols, rows, depth);
queue->enqueueNDRangeKernel(kernel, offset, global, local);
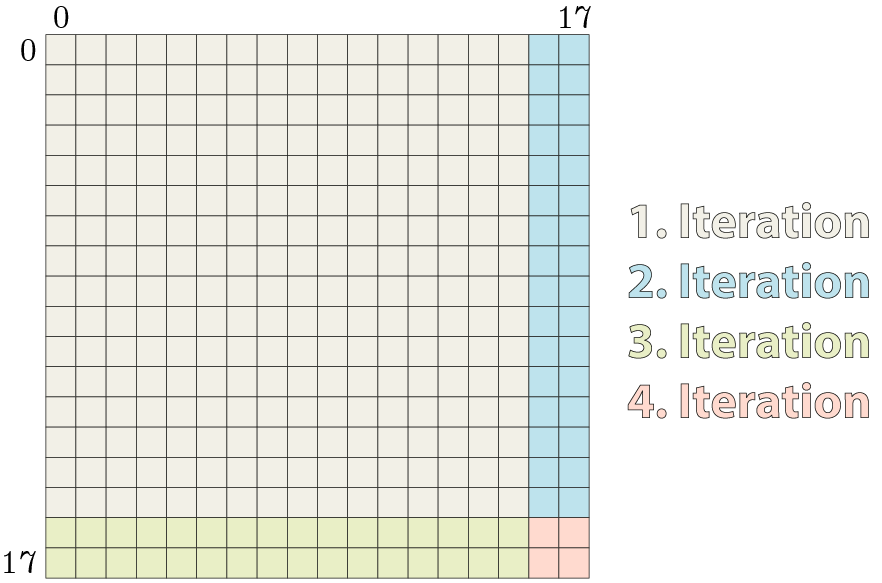
Note the used offset which stores the number of previous images (e.g. 8 in the octave = 2 iteration) and depth = 4 which makes this kernel a 3D problem: the filter is computed for all image pixels in all four images of the current octave.
The code for images and cubes is not very exciting, so I will not show any details for them. Check out the implementation if you want to know more.
Benchmark
It is now time to do some benchmarking. I start by testing a normal filter operation (called single in the related article). A short summary of the implementation is: unrolling and constant memory is used for the filter but no other optimizations. The first thing I want to test is the difference between the default local work-group size, i.e. setting the corresponding parameter to cl::NullRange, and the size manually to \(16 \times 16\). This is a common block size for an image patch computed by a work-group and is also the maximum possible size on my AMD R9 290 GPU. It turns out that this setting is quite crucial for buffers as you can see in the next figure.
It really is important to manually set the local work-group size for buffers. Performance totally breaks for larger filters. The fact that a fixed size increases the speed that much is, I think, indeed evidence that buffers use the cache hierarchy. Otherwise, the local size shouldn't matter that much. But, there are still some differences compared to image buffers. Even though they also profit from a manually set work-group size, the effect is not that huge. Maybe the texture address units do some additional stuff not mentioned here which helps to increase cache performance. I don't think that it is related to some processing in the texture filter units since there is not much left. No type conversion must be done and a sampler can't be used for image buffers anyway. Additionally, the address calculation (\(cols*y + x\)) is done in both buffers inside the kernel and therefore executed by the SIMD units. Another possibility would be that the local work-group size is set differently for image buffers than for normal buffers. Unfortunately, I don't know of a way to extract this size when not set explicitly (the profiler just shows NULL).
If you compare the image buffers with one of the other image types (e.g. images), you see that image buffers are a bit slower. This is the effect of the missing sampler and the address calculation which needs to be done manually for image buffers. So, if possible, you should still prefer the normal image type over image buffers. But let me note that sometimes it is not possible or desired to work with 2D image objects. For example, let's say you have a point structure like
struct KeyPoint
{
int octave;
int level;
float x;
float y;
};
and you want to store a list of points which can be located anywhere in the image pyramid. Suppose further you want later (e.g. in a different kernel call) access the image pixels and its neighbours. Then you need to have access to the complete image pyramid inside the kernel and not only to a specific image. This is only possible when the pyramid is stored in an (image) buffer because then you can read pixels from all levels at once.
Another noticeable comparison is between images and cubes. First, the local work-group size does not play an important role in both cases. The differences here are negligible. It is likely that the hardware has more room for optimization since it knows which pixels in the 2D image plane are accessed. Remember that bot \(x\) and \(y\) are provided to the access functions. Second, cubes are consistently slower than images. Even though cubes can be executed with only 4 instead of 16 kernel calls and hence results in less communication with the driver and therefore less overhead. Maybe cubes are too large and stress the caches too much so that the benefit of the kernel calls are neutralized. Anyway, this is precisely the reason why I decided to use images and not cubes to store my pyramid.
The next thing I want to assess is the benefit of local memory. The following chart compares the results for fixed size work-groups from before with the case that always local memory is used (implementation details about how to use local memory for this task are shown in the filter evaluation article).
It is clear that local memory is beneficial for filter sizes \(\geq 5 \times 5\) regardless of the storage type. This is not surprising though since local memory is still faster than the L1 cache. Additionally, the L1 cache is smaller (16 KB L1 vs. 64 KB LDS), so it is to be expected that for larger filters performance decreases. For a filter of size \(3 \times 3\) the situation is not that clear. Sometimes it is faster and sometimes not. Don't forget that the manual caching with local memory does also introduce overhead. The data must be copied to the LDS and read back by the SIMD units. In general, I would say that it is not worth to use local memory for such a small filter.
Considering only the lines which use local memory, the result looks a bit messy. No clear winner and crossings all over again. I decided to use normal image types since they are easy to handle and offer full configuration via the sampler object. But I would also recommend that you test this on your own hardware. The results are very likely to differ.