Es gibt mehrere Möglichkeiten, wie definiert werden kann, ob ein natürliches Monopol vorliegt oder nicht. Eine davon ist die Verwendung der Subadditivität. Dabei geht man davon aus, dass die Kostenstruktur und damit die Kostenfunktion für die Herstellung des Produktes bekannt sind. Zumindest wenn man mit der Definition auch rechnen möchte. Grundsätzlich besteht das Ziel dabei darin, mit Hilfe der Kostenfunktionen eine bestimmte Menge herzustellen. Die Frage ist nun, ob es günstiger ist, wenn nur ein oder wenn mehrere Unternehmen die gewünschte Menge produzieren.
Dies hängt insbesondere von der Kostenstruktur ab, die bestimmt, welche Kosten anfallen, um ein Gut in einer bestimmten Menge zu produzieren. Sind die Fixkosten hoch, so spricht die Kostenstruktur eher für ein Monopol. Falls es jedoch nichtlineare variablen Kosten gibt (z. B. wegen Kapazitätsbeschränkungen), so kann es sich auch lohnen, wenn mehrere Unternehmen ein Gut produzieren und sich somit die Gesamtmenge des Marktes aufteilen (mathematisch die Menge, die in die Kostenfunktion eingesetzt wird).
Im Rahmen der Subadditivität werden nun einfach zwei Kosten miteinander verglichen: zum einen die Kosten, wenn ein Unternehmen die gesamte Menge produziert (Monopol) und zum anderen wenn die Gesamtmenge gleichmäßig zwischen \(n\) produzierenden Unternehmen aufgeteilt wird. Sind für eine gegebene Menge \(x\) die Kosten im ersten Fall geringer, so liegt ein natürliches Monopol vor, ansonsten nicht:
\begin{equation} \label{eq:MonopolSubadditivitaet_Subadditivitaet} K(x) < \sum_{i=1}^n K(x_i) \quad \text{mit} \quad x = \sum_{i=1}^n x_i. \end{equation}Wenn die Ungleichung erfüllt ist, handelt es sich um ein natürliches Monopol. Häufig, wie auch in diesem Übungsblatt, stellt sich die Frage nach dem Monopol gar nicht für eine bestimmte Menge, sondern es ist eher gesucht, ab welcher Menge ein Umschwung stattfindet. Oder anders ausgedrückt: ab welcher Menge herrscht Gleichheit in den Kosten?
Im Falle eines Duopols reduziert sich \eqref{eq:MonopolSubadditivitaet_Subadditivitaet} damit zu
\begin{equation} \label{eq:MonopolSubadditivitaet_KostenDuopol} K(x) < K\left( \frac{x}{2} \right) + K\left( \frac{x}{2} \right), \end{equation}da davon ausgegangen wird, dass im Duopol beide Unternehmen sich die Menge gleichmäßig aufteilen. Für die Kostenfunktion aus der Übung
\begin{equation*} K(x) = 400 + x^2 \end{equation*}lässt sich der Schnittpunkt direkt ausrechnen
\begin{align*} K(x) &= K\left( \frac{x}{2} \right) + K\left( \frac{x}{2} \right) \\ 400 + x^2 &= 400 + \left(\frac{x}{2}\right)^2 + 400 + \left(\frac{x}{2}\right)^2 \\ x^2 &= 400 + \frac{x^2}{4} + \frac{x^2}{4} \\ x^2 &= 400 + \frac{x^2}{2} \\ \frac{x^2}{2} &= 400 \\ x^2 &= 800 \\ x &= \pm \sqrt{800} \Rightarrow 20 \sqrt{2}. \end{align*}Da wir keine negative Menge produzieren wollen, ist natürlich nur der positive Betrag von Belang. Auch ein Plot der beiden Funktionen offenbart den berechneten Schnittpunkt und zeigt auf, welche unnötigen Kosten links bzw. rechts davon entstehen können (schraffierte Bereiche).
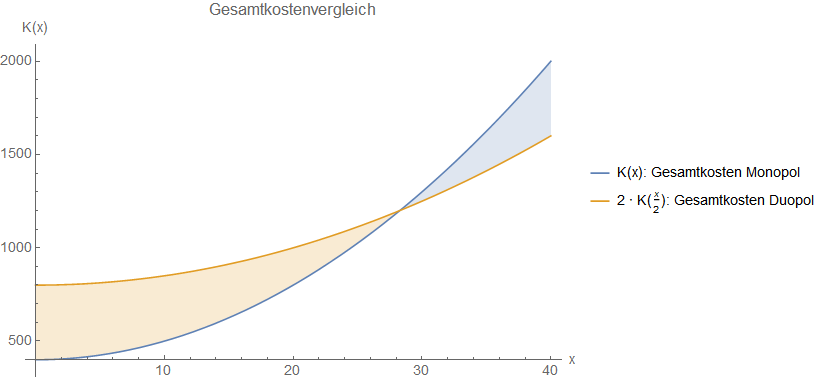
In diesem Fall gibt es zwei Quellen, die hier gegeneinander antreten und diese Kostenstruktur verursachen. Zum einen haben wir Fixkosten von 400, die z. B. durch Maschinen hervorgerufen werden können. Jedes Unternehmen muss seine eigenen Maschinen kaufen, daher ist es bei einer niedrigen Menge noch günstiger, wenn es nur ein Unternehmen auf dem Markt gibt. Zum anderen ist da jedoch noch der quadratische Kostenterm \(x^2\), welcher genau in die gegensätzliche Richtung wirkt. Hier wird es umso teurer, je größer die zu produzierende Menge wird. Ab einem bestimmten Punkt lohnt sich das Monopol daher nicht mehr.
Man kann noch einen Schritt weitergehen und sich die Kostenstruktur auch anhand der durchschnittlichen Kosten veranschaulichen (so wie in der Übung getan). Dazu wird \eqref{eq:MonopolSubadditivitaet_KostenDuopol} als Gleichung behandelt und umgeformt zu
\begin{align*} K(x) &= K\left( \frac{x}{2} \right) + K\left( \frac{x}{2} \right) \\ DK(x) \cdot x &= DK\left( \frac{x}{2} \right) \cdot \frac{x}{2} + DK\left( \frac{x}{2} \right) \cdot \frac{x}{2} \\ DK(x) \cdot x &= DK\left( \frac{x}{2} \right) \cdot x \\ DK(x) &= DK\left( \frac{x}{2} \right). \\ \end{align*}Es werden also zwei Punkte entlang der Durchschnittskostenfunktion gesucht, bei der im Monopol die gleichen durchschnittlichen Kosten pro Einheit anfallen wie im Duopol. Denn dann ist es z. B. egal, ob ein Unternehmen 100 Stück zu Kosten von 10 € pro Stück produziert oder ob zwei Unternehmen jeweils 50 Stück produzieren aber auch nur Kosten von 10 € pro Stück haben. Der Ansatz ist identisch zum Gesamtkostenvergleich und führt daher auch zur gleichen kritischen Menge
\begin{align*} DK(x) &= DK\left( \frac{x}{2} \right) \\ \frac{400}{x} + x &= \frac{400}{0.5x} + \frac{x}{2} \\ \frac{400}{x} + x &= \frac{800}{x} + \frac{x}{2} \\ \frac{x}{2} &= \frac{400}{x} \\ x &= \frac{800}{x} \\ x^2 &= 800 \Rightarrow 20 \sqrt{2}. \end{align*}Die grundsätzliche Idee lässt sich auch noch einmal in der folgenden Animation zusammenfassen. Dabei wird eine bestimmte Menge \(x_p\) gewählt und dann verglichen, welche Kosten bei einem Unternehmen (Monopol, Dreieck) und welche Kosten bei zwei Unternehmen (Duopol, Kreis) entstehen. Es ist dabei zu sehen, dass links von der waagrechten roten Linie das Monopol noch günstiger ist (Dreieck liegt unter dem Kreis). Hier überwiegen noch die hohen Fixkosten, welche sich erst einmal rechnen müssen. Nach dem vorbeiziehen an der roten Linie lohnt sich dann das Duopol (Kreis liegt unter dem Dreieck). In diesem Bereich überwiegt nun der quadratische Kostenterm.
List of attached files:
- MonopolSubadditivitaet.nb [PDF] (Mathematica-Notebook mit welchem die Grafik und die Animation erstellt wurde)
← Back to the overview page